Llargor

Llargor
naturaleza de una magnitud (es) y cantidad base del SI (es)
propiedá física escalar, geometric measure (en) y Distancia
Llargor área

La llargor ye un concepto métricu definible pa entidaes xeométriques sobre la que se definió una distancia. Más concretamente dau un segmentu, curva o llinia fina, puede definise el so llargor a partir de la noción de distancia. Sicasí, nun tien de confundir se llargor con distancia, yá que pa una curva xeneral (non pa un segmentu rectu) la distancia ente dos puntos cualesquier de la mesma ye siempres inferior al llargor de la curva entendida ente esos dos puntos. Igualmente la noción matemática de llargor puede identificase cola una magnitú física que determinada pola distancia física.

El llargor ye una de les magnitúes físiques fundamentales, en cuantes que nun puede ser definida en términos d'otres magnitúes que pueden midise. En munchos sistemes de midida, el llargor ye una magnitú fundamental, de la cual deriven otres.^[1]

El llargor ye una midida d'una dimensión (llinial; por casu la distancia en m), ente que el área ye una midida de dos dimensiones (al cuadráu; por casu m²), y el volume ye una midida de tres dimensiones (cúbica; por casu m³).

Sicasí, según la teoría especial de la relatividá (Albert Einstein, 1905), el llargor nun ye una propiedá intrínseca de nengún oxetu yá que dos observadores podríen midir el mesmu oxetu y llograr resultancies distintes (contraición de Lorentz).^[2]

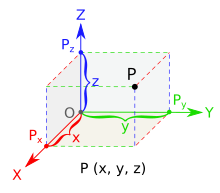
El llargu o llargor dimensional d'un oxetu ye la midida de la so exa tridimensional y. Esta ye la manera tradicional en que se nomaba a la parte más llarga d'un oxetu (tocantes a la so base horizontal y non el so altu vertical). En coordenaes cartesianes bidimensionales, onde solo esisten les exes xy nun se denomina «llargu». Los valores x indiquen l'anchu (exa horizontal), y los y l'altu (exa vertical).^[3]

1. ↑ Resnick, 1993, pp. 1-3.
2. ↑ Resnick, 1993, p. 524.
3. ↑ García Prieto, F. J. (2012). Matemátiques 2º Y.S.O.. Editex, páx. 198. ISBN 9788490033340.